Giải pháp mô phỏng phổ đáp ứng

Phân tích phổ đáp ứng thường được sử dụng cho trường hợp phân tích đáp ứng của kết cấu dưới tác dụng của tải thay đổi theo thời gian đã biết. Kết quả phân tích giúp xác định các đáp ứng của kết cấu trong các điều kiện tải ngẫu nhiên hoặc tải phụ thuộc thời gian như là: tải động đất, tải trọng gió, tải trọng sóng biển, tải trọng sinh ra trong quá trình hoạt động của động cơ phản lực, v.v…

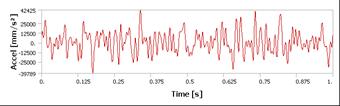
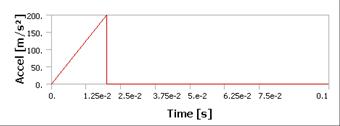
Để thu được lời giải chính xác cho một bài toán đáp ứng động lực học của kết cấu bằng phương pháp mô phỏng số, chúng ta phải thực hiện một phân tích vừa lớn và vừa dài theo thời gian. Ở đây, lớn có nghĩa là sử dụng mô hình chính xác, nhiều bậc tự do. Còn dài ở đây có nghĩa là cần nhiều điểm thời gian để xác định trạng thái của hệ kết cấu. Bằng cách này chúng ta sẽ tốn nhiều thời gian và tài nguyên máy tính để giải quyết bài toán.

Thay vì phải giải một bài toán tốn kém như vậy, chúng ta hoàn toàn có thể xấp xỉ đáp ứng động lực học lớn nhất một cách nhanh chóng bằng phương pháp phổ đáp ứng (Response Spectrum). Phương pháp này sử dụng các kết quả từ phân tích rung động/dao đông tự nhiên (Modal Analysis), và một phổ tải đầu vào đã biết để tính toán các đại lượng chuyển vị, ứng suất trong mô hình kết cấu.

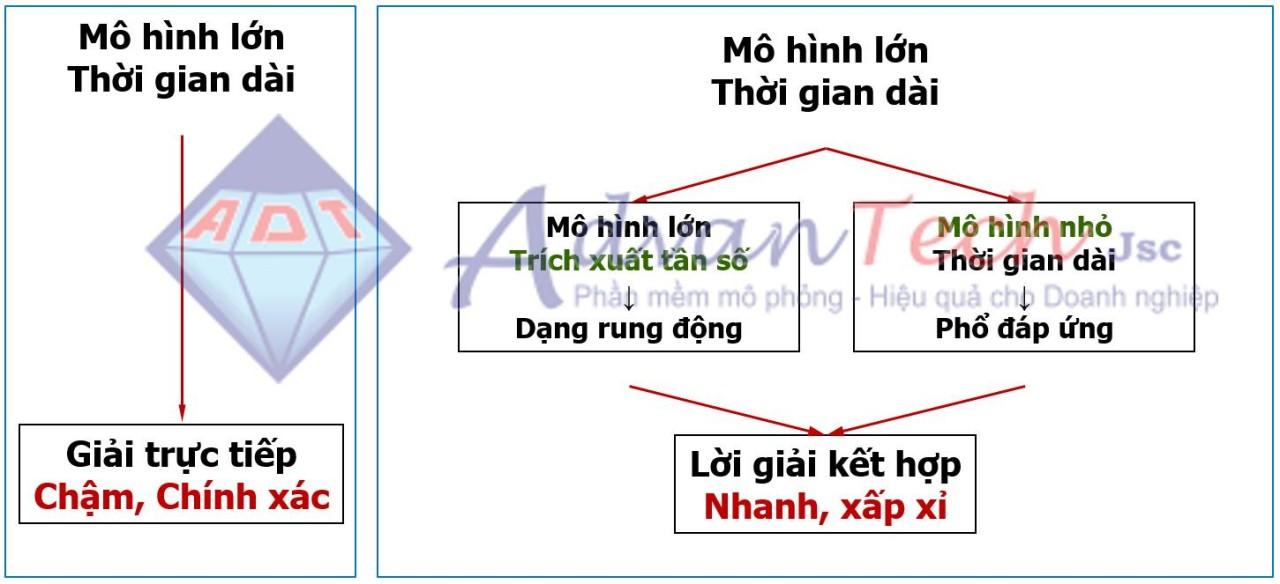
Phổ tải đầu vào ở đây là một đồ thị quan hệ giữa giá trị phổ và tần số - ghi lại cường độ và tần số của các thành phần tải theo thời gian đã biết. Quá trình tạo phổ đáp ứng theo thời gian sử dụng một loạt các bộ rung động 1 bậc tự do đơn giản, có các tần số rung động tự nhiên khác nhau.

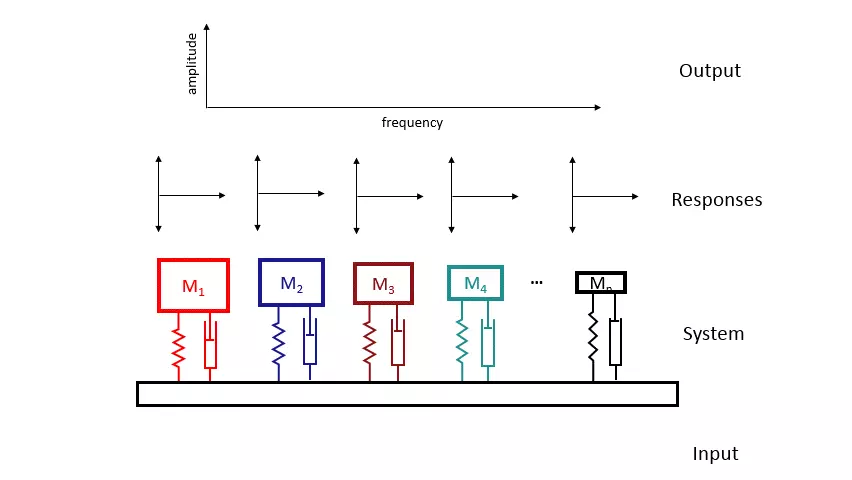
Cách thức thực hiện một bài toán phổ đáp ứng:
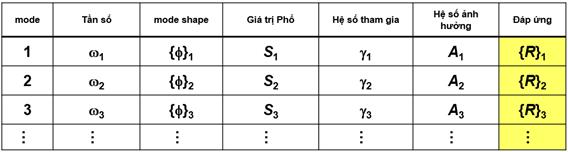
      1. Xác định các mode rung động tự nhiên (ωi và mode shape {ϕ}i) tham gia tạo ra đáp ứng của hệ kết cấu.
      2. Xác định hệ số ảnh hưởng (γi) của các mode tần số rung động tự nhiên đến đáp ứng tổng của kết cấu.
      3. Xác định giá trị phổ (Si) ứng với từng giá trị tần số bằng cách tra đáp ứng từ đường phổ đáp ứng.
      4. Xác định hệ số Mode (Mode Coefficient) của từng mode tần số theo công thức Ai = Si x γi.
      5. Xác định đáp ứng thành phần {R}i ứng với từng mode tần số: {R}i = Ai x {ϕ}i.
      6. Tổng hợp đáp ứng của hệ từ các đáp ứng thành phần {R}i sử dụng phương pháp phù hợp.

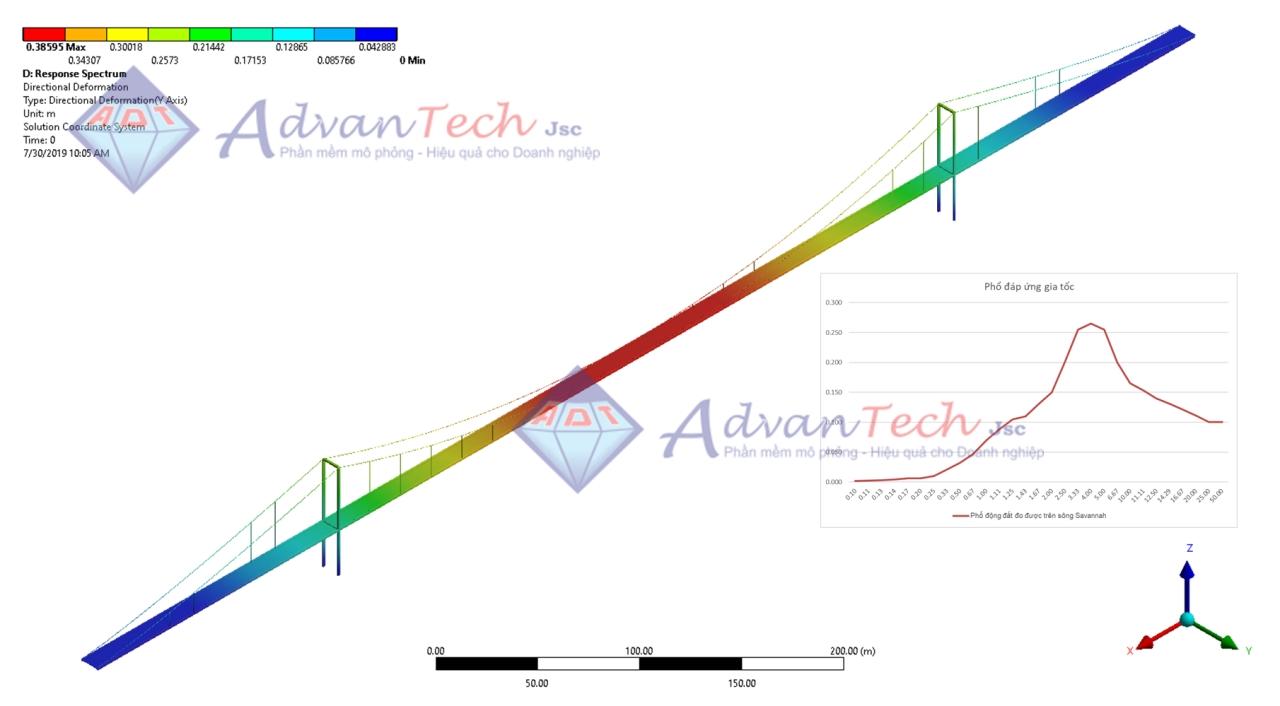
Như đã nói ở phía trên, Phân tích Phổ đáp ứng phù hợp với các trường hợp mô phỏng đáp ứng động lực học theo thời gian cho mô hình lớn, phức tạp. Phương pháp này sẽ giúp cho các kỹ sư tiết kiệm được chi phí tài nguyên tính toán và thời gian phân tích mà vẫn đảm bảo được độ an toàn chất lượng sản phẩm/công trình.

Nhìn chung, tính toán mô phỏng số nói chung sẽ giúp các đơn vị tạo tính đột biết trong sáng tạo, đẩy nhanh quá trình thiết kế và sản xuất, nhanh chóng đưa sản phẩm ra thị trường, tạo tính cạnh tranh cho sản phẩm.